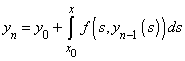
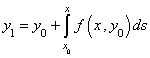
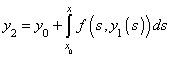
La suite des approximations successives de Picard est obtenue à partir de la formule : On utilise la variable x comme borne supérieure de l'intégrale et on utilise la variable s comme variable d'intégration.     On obtient :     et ainsi de suite. L'application de cette méthode demande de pouvoir effectivement trouver une primitive à chaque itération, ce qui n'est possible que pour certains cas très simples. La méthode a plutôt servi de base pour montrer l'existence d'une solution, même dans les cas où on n'est pas capable de déterminer celle-ci. 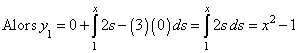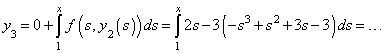------------------------------------------------- Exemple : Effectuons quelques itérations de Picard pour résoudre l'équation différentielle ------------------------------------------------- Exemple d'application de la méthode des itérations de Picard avec le logiciel Maple. Pour voir les commandes Maple même si vous n'avez pas le logiciel, voici la version HTML du fichier précédent. Exemple d'application de la méthode des itérations de Picard avec le logiciel Derive Pour voir les commandes Derive même si vous n'avez pas le logiciel, voici la version PDF du fichier précédent. Voyez le texte suivant, pour un exemple d'application de la méthode d'itérations de Picard avec la calculatrice symbolique TI-92 Plus ou TI-89. -------------------------------------------------